使用java语言产生素数-译

发表于 | 分类于 | | 浏览 次
字数统计: 2.4k | 阅读时长 ≈ 11

文章来源： Generating Prime Numbers in Java

作者： baeldung

Generating Prime Numbers in Java

1. Introduction 简介

In this tutorial, we’ll show various ways in which we can generate prime numbers using Java.

在本教程中，我将会使用java给你展示几种不同的素数生成方法。

If you’re looking to check if a number is prime – here’s a quick guide on how to do that.

假如你正需要验证一个数字是否为素数 - 这是一个快速判定素数的指南。

2. Prime Numbers 素数

Let’s start with the core definition. A prime number is a natural number greater than one that has no positive divisors other than one and itself.

让我们从最核心的定义开始，一个素数就是只能被自身或者1整除的大于1的自然数。

For example, 7 is prime because 1 and 7 are its only positive integer factors, whereas 12 is not because it has the divisors 3 and 2 in addition to 1, 4 and 6.

举个栗子，7是个素数，因为它只能被1和7整除。然而12就不是一个素数，因为它能被1,4,6和2,3整除。

3. Generating Prime Numbers 生成素数

In this section, we’ll see how we can generate prime numbers efficiently that are lower than a given value.

在这一部分，我们将会了解怎样生成小于给定数值的素数。

3.1. Java 7 And Before – Brute Force Java7以及Java7之前，使用蛮力产生素数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
public static List<Integer> primeNumbersBruteForce(int n) {
    List<Integer> primeNumbers = new LinkedList<>();
    for (int i = 2; i <= n; i++) {
        if (isPrimeBruteForce(i)) {
            primeNumbers.add(i);
        }
    }
    return primeNumbers;
}
public static boolean isPrimeBruteForce(int number) {
    for (int i = 2; i < number; i++) {
        if (number % i == 0) {
            return false;
        }
    }
    return true;
}

As you can see, primeNumbersBruteForce is iterating over the numbers from 2 to n and simply calling the isPrimeBruteForce() method to check if a number is prime or not.

正如你所看到的，primeNumbersBruteForce函数迭代从2到n之间的数，并且在每次迭代中简单地调用isPrimeBruteForce()函数来检查一个数字是否为素数。

The method checks each numbers divisibility by the numbers in a range from 2 till number-1.

isPrimeBruteForce函数检查每个数字是否能被2到number-1之间的数字整除。

If at any point we encounter a number that is divisible, we return false. At the end when we find that number is not divisible by any of its prior number, we return true indicating its a prime number.

如果我们遇到任何一个能被整除的数字，就会之间返回false。最后就能找到那个不能被除自身和1之外的数字整除的那个数，然后函数返回true，表示这是一个素数。

3.2. Efficiency And Optimization 效率和优化

The previous algorithm is not linear and has the time complexity of O(n^2). The algorithm is also not efficient and there’s clearly a room for improvement.

上面的算法不是线性，它的时间复杂度是O(n²)。这个算法也并不高效，有很明显的效率提升空间。

Let’s look at the condition in the isPrimeBruteForce() method.

让我们看一下isPrimeBruteForce()函数中的判断条件。

When a number is not a prime, this number can be factored into two factors namely a and b i.e. number = a b. **If both a and b were greater than the square root of n, a\b would be greater than n.**

当一个数字不是素数时，这个数字能够分解为a b形式的两个数字，即number = a b。如果a和b都比n的平方根大，那么a*b的结果就比n打

So at least one of those factors must be less than or equal the square root of a number and to check if a number is prime, we only need to test for factors lower than or equal to the square root of the number being checked.

所以两个因数中至少有一个比这个数字的平方跟小或者与之相等，并且要检查一个数字是否为素数，我们只需要检查小于或者等于待检测数字的平方根的那些因数即可。

Additionally, prime numbers can never be an even number as even numbers are all divisible by 2.

另外，素数永远不可能是偶数，因为偶数总是能被2整除。

Keeping in mind above ideas, let’s improve the algorithm:

请牢记上面这个思路，下面我们改进一下这个算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
public static List<Integer> primeNumbersBruteForce(int n) {
    List<Integer> primeNumbers = new LinkedList<>();
    if (n >= 2) {
        primeNumbers.add(2);
    }
    for (int i = 3; i <= n; i += 2) {
        if (isPrimeBruteForce(i)) {
            primeNumbers.add(i);
        }
    }
    return primeNumbers;
}
private static boolean isPrimeBruteForce(int number) {
    for (int i = 2; i*i < number; i++) {
        if (number % i == 0) {
            return false;
        }
    }
    return true;
}

3.3. Using Java 8 使用Java8

Let’s see how we can rewrite the previous solution using Java 8 idioms:

我们来看一下使用Java8来重写上面逻辑的常见用法：

1
2
3
4
5
6
7
8
9
10
public static List<Integer> primeNumbersTill(int n) {
    return IntStream.rangeClosed(2, n)
      .filter(x -> isPrime(x)).boxed()
      .collect(Collectors.toList());
}
private static boolean isPrime(int number) {
    return IntStream.rangeClosed(2, (int) (Math.sqrt(number)))
      .filter(n -> (n & 0X1) != 0)
      .allMatch(n -> x % n != 0);
}

3.4. Using Sieve Of Eratosthenes 使用埃拉托斯特尼筛法

埃拉托斯特尼筛法（希腊语：κόσκινον Ἐρατοσθένους，英语：sieve of Eratosthenes ），简称埃氏筛，也称素数筛。这是一种简单且历史悠久的筛法，用来找出一定范围内所有的素数。所使用的原理是从2开始，将每个素数的各个倍数，标记成合数。一个素数的各个倍数，是一个差为此素数本身的等差数列。此为这个筛法和试除法不同的关键之处，后者是以素数来测试每个待测数能否被整除。埃拉托斯特尼筛法是列出所有小素数最有效的方法之一，其名字来自于古希腊数学家埃拉托斯特尼，并且被描述在另一位古希腊数学家尼科马库斯所著的《算术入门》中。

There’s yet another efficient method which could help us to generate prime numbers efficiently, and it’s called Sieve Of Eratosthenes. Its time efficiency is O(n logn).

还有一种高效的方法能够帮助我们生成素数，这种方法叫埃拉托斯特尼筛法。它的时间复杂度是O(nlogn)。

Let’s take a look at the steps of this algorithm:

我们看一下这个算法的步骤：

  1. Create a list of consecutive integers from 2 to n: (2, 3, 4, …, n)

    从2到n生成一个连续的整数列表

  2. Initially, let p be equal 2, the first prime number

    最初状态下，令p等于2，也就是第一个素数。

  3. Starting from p, count up in increments of p and mark each of these numbers greater than p itself in the list. These numbers will be 2p, 3p, 4p, etc.; note that some of them may have already been marked

    从p开始，以p为增量进行计数，并将以p为增量计数形成的列表中的所有大于p的值标记起来，这些数字将会是2p，3p，4p等等的一些数字，注意，这里面的一些数字可能之前已经被标记过。

  4. Find the first number greater than p in the list that is not marked. If there was no such number, stop. Otherwise, let p now equal this number (which is the next prime), and repeat from step 3

    从2到根号n中找出第一个大于p而没有没被标记的数字，如果找不到，就结束查找，否则，就令p等于这个数（这就是下一个素数），然后重复步骤3.

At the end when the algorithm terminates, all the numbers in the list that are not marked are the prime numbers.

在算法最终结束的时候，在2到n这个列表中所有未被标记的数字就是所有的素数。

Here’s what the code looks like:

看一眼代码是怎样写的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
public static List<Integer> sieveOfEratosthenes(int n) {
    boolean prime[] = new boolean[n + 1];
    Arrays.fill(prime, true);
    for (int p = 2; p * p <= n; p++) {
        if (prime[p]) {
            for (int i = p * 2; i <= n; i += p) {
                prime[i] = false;
            }
        }
    }
    List<Integer> primeNumbers = new LinkedList<>();
    for (int i = 2; i <= n; i++) {
        if (prime[i]) {
            primeNumbers.add(i);
        }
    }
    return primeNumbers;
}

3.5. Working Example of Sieve Of Eratosthenes 埃拉托斯特尼筛法的工作实例

Let’s see how it works for n=30.

我们看一下n=30的情况下是如何工作的。

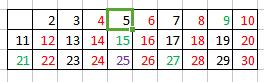
example

Consider the image above, here are the passes made by the algorithm:

就上面这个图片来说，下面是通过这个算法验证的数：

  1. The loop starts with 2, so we leave 2 unmarked and mark all the divisors of 2. It’s marked in image with the red color

    循环从2开始，所以我们不标记2，而是标记所有能被2整除的数，就是上面图片中所有红色标记的数字。

  2. The loop moves to 3, so we leave 3 unmarked and mark all the divisors of 3 not already marked. It’s marked in image with the green color

    循环走到了3这里，我们将3设置为非标记状态，然后将所有能被3整除但是还没有被标记的的数都标记起来，就是上面图片中使用绿色标记的数字。

  3. Loop moves to 4, it’s already marked, so we continue

    循环来到4这里，4已经被标记了，所以就跳过，然后循环继续。

  4. Loop moves to 5, so we leave 5 unmarked and mark all the divisors of 5 not already marked. It’s marked in image with the purple color

    循环来到5这里，我们将5设置为非标记状态，然后将所有能被5整除但是还有没被标记的数字标记起来，就是图片中的紫色的数字。

  5. We continue above steps until loop is reached equal to square root of n

    重复上面的步骤直到循环变量大于或等于根号n。

4. Conclusion 总结

In this quick tutorial, we illustrated ways in which we can generate prime numbers until ‘N’ value.

在这个简短的教程中，我们指出了多种生成N值之下的所有素数的方式。

The implementation of these examples can be found over on GitHub.

可以在Github上找到这些实例的具体实现方法。